
我们提供安全,免费的手游软件下载!
Demosaic,中文直接发翻译为去马赛克, 但是其本质上并不是去除马赛克,这让很多第一次接触这个名词或者概念的人总会想的更多。因此,一般传感器在采集信息时一个位置只采集RGB颜色中的一个通道,这样可以减少采集量,降低成本,由于人的视觉对绿色最为敏感,所以一般情况下,绿色分量会比红色和蓝色分量多一倍的信息,这样,根据RGB不同的位置排布,就产生了RGGB、GBRG、GRBG、BGGR四种常用的模式,比如RGGB模式就如下所示:
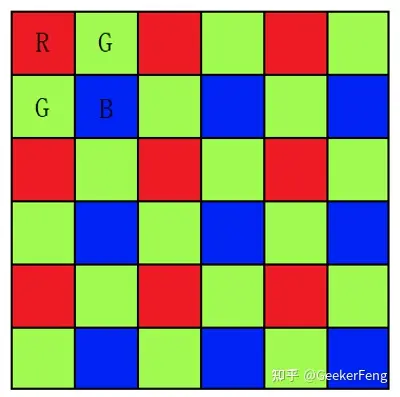
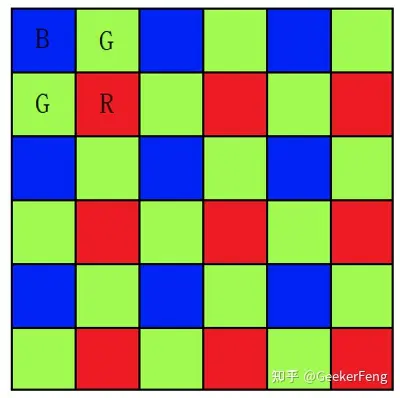
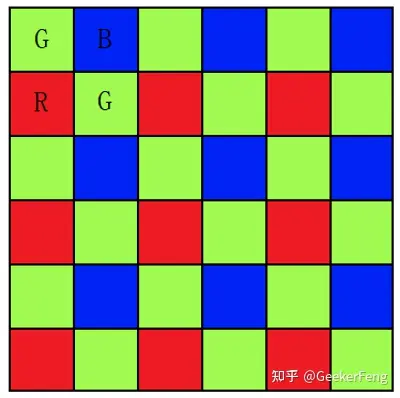
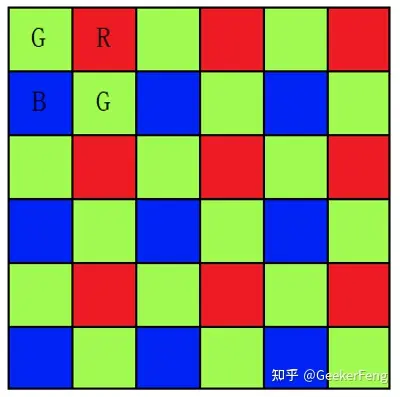
RGGB BGGR GBRG GRBG
去马赛克的目的就是从这些确实的信息中尽量的完美的复原原始信息,比如上图第一个点,只有红色分量是准确的,那就要想办法通过其他的信息重构出改点的绿色和蓝色分量。
目前,关于这方面的资料也是很多的,这里我描述下目前我已经优化和处理的四个算法,并分享部分代码。
一、双线性处理
一个最为直接和简单的想法就是利用领域的相关信息通过插值来弥补当前缺失的颜色分量,我们以RGGB格式为例,参考上图(坐标都是从0开始,X轴从左向右递增,Y轴从上向下递增)。
先不考虑边缘。
比如(1,1)坐标这个点,现在已经有了B这个分量,缺少R和G这个分量,但是他四个对角线上都有R分量,因此,可以使用这个4个像素的平均值来计算改点的R分量,而在其上下左右四个方向有恰好有4个点的G分量,同理可以用这个四个的平均值来评估当前点的G值。
在考虑(1,2)这个坐标点,他的当前有效值是G分量,缺少R和B分量,而他则没有(1,1)点那么幸运,他周边的有效R和B分量都只有2个,因此,只能利用这两个有效值的平均值来评估该点的R/B分量。
其他的点类似处理。
在考虑边缘,由于边缘处的像素总有某一个方向或某二个方向缺少像素,因此,可以利用镜像的关系把缺少的那一边取镜像的位置信息来补充。
一个简单的高效的C++代码如下所示:
这个算法是非常高效的,而且极易使用指令集优化,在一台普通的配置的PC上(12th Gen Intel(R) Core(TM) i7-12700F 2.10 GHz)处理1902*1080的图,大概只需要2ms,SSE优化后可以做到0.6ms,但是这个方法忽略边缘结构和通道间的相关性,从而容易导致颜色伪彩和图像模糊,比如下面这个经典的测试图,解码后的结果有点惨不忍睹。


用彩色显示RGGB格式图(即把其他通道的颜色分量设计为0) 双线性解码后的结果
在解码后的水平和垂直方向栅栏中都可以看到明显的色彩异常。
但是由于这个算法的极度高效性,在有些要求不高的场合,依旧可以使用该算法。
二、Hamilton-Adams算法
这也是个非常经典的算法,在说明这个算法之前,必须说明下色差恒定理论。
色差恒定准则与色比恒定准则都是基于颜色通道之间的相关性,目的都是把颜色通道之间的相关性信息引入颜色插值算法,提高插值的准确性。色差相比于色比有两点优势:
第一,色差的运算简单,更容易实现。第二, 色比在G通道接近0时误差较大,色差不存在这类问题。因此,绝大多数颜色插值算法中使用了色差。
那么色差恒定理论,其最为核心的思想就是:临近的两个彩色像素,其相同颜色分量之间的差异值应该近似差不多,用公式表示如下:
R(X,Y) - R(X-1,Y) = G(X,Y) - G(X-1,Y) = B(X,Y) - B(X-1,Y)
那这是时候如果我们已经获取了某个颜色通道的所有位置的值,通过这个公式就很容易推导出其他位置缺失的值了。
我们还是以上面的(1,1)坐标点为例,假定我们已经获取了所有G通道的数据,也就是说这个(1,1)这个点实际只有R通道数据缺失了(B数据本身就有),这个时候根据颜色恒差理论,应该有
R(1,1) - R(0,0) = G(1,1) - G(0,0) ------> R(1,1) = G(1,1) + R(0,0) - G(0, 0)
实际上满足这个等式还有(0,2)、(2,0)、(2,2)这三个点(这三个点的红色分量是准确值),所以为了得到更好的精度,我们可以通过下式最终确定R(1,1)的值。
R(1,1) = (G(1,1) + R(0,0) - G(0, 0) + G(1,1) + R(0,2) - G(0, 2) + G(1,1) + R(2,0) - G(2, 0) + G(1,1) + R(2,2) - G(2, 2)) /4
整理后即为:
R(1,1) = G(1,1) + (R(0,0) + R(0,2) + R(2, 0) + R(2,2) - G(0,0) -G(0,2) -G(2, 0) -G(2,2)) / 4
对于(1,2)这个点,G通道数据本来就有,缺少R和B,那根据颜色恒差理论,应该有
R(1,2) - G(1,2) = R(0,2) - G(0,2)
B(1,2) - G(1,2) = B(1,1) - G(1,1)
同样的道理,还有
R(1,2) - G(1,2) = R(2,2) - G(2,2)
B(1,2) - G(1,2) = B(1,3) - G(1,3)
类似(1,2)的方法,把他们综合起来可以得到更为精确的结果:
R(1,2) = G(1,2) + ((R(0,2) + R(2,2) - G(0,2) - G(2,2)) / 2
B(1,2) = G(1,2) + ((B(1,1) + B(1,3) - G(0,2) - G(2,2)) / 2
以上利用颜色恒差理论,就把各个通道之间的数据关联了起来。那么前面的计算都有一个前提条件,就是绿色通道的数据都已经知道了。
我们前面说过,绿色通道的数据量本身只缺少了一半,而缺少了那一半中任何一个点的数据都可以用周边四个点的领域数据填充,因此,如果我们绿色通道就这样处理,而红色和蓝色则用颜色恒差理论借助绿色通道的数据后结果如何呢,我们就把这样做的算法叫做CDCT把,一个简单的严重这个算法的代码如下所示:
其中 IM_RGGB_CalcRed_CDCT_PureC代码如下所示:
IM_RGGB_CalcBlue_CDCT_PureC是类似的道理。
经过测试,这样做的结果和直接双线性相比,基本没有什么差异的,所以直接这样还是不行的,
Hamilton-Adams等人在结合绿色通道的一阶导数和周边红色和蓝色的通道的二阶倒数的基础上,对绿色分量的插值提出了如下算法,这个过程考虑到了像素之间的边缘信息:

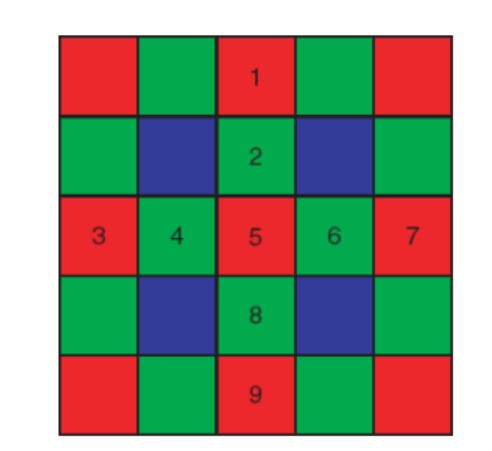
当水平方向的梯度大于垂直方向的梯度时,使用垂直方向的有关像素计算结果,否则使用水平方形的有关值,如果两者相等,则使用平均值。
实际操作时,都会定义一个阈值,如果水平和垂直的梯度之差的绝对值小于阈值,则使用平均值,如果在阈值之外,再考虑水平和垂直之间的关系。这样能获得更为合理的结果。
实际上,仔细看看,上面每个方向的G5的计算也是利用到了颜色恒差理论的,只是只是单独利用了水平或者垂直方向的像素而已。
我们分享一下更具上述思路编写的C++代码结果:
我们分享下前面说的CDCT算法以及HamiltonAdams算法的结果:


简单的CDCT结果 HamiltonAdams结果
从上面右图的结果可以看到,相比于双线性,水平栅栏处似乎已经看不到色彩异常了,垂直栅栏处的异常点也大为减少,但是还是存在些许瑕疵。
在速度方面,由于直接使用双线性时,可以直接把数据数据有规律的填充到目的图中,而且计算量很简单,而使用色差恒定理论后,由于顺序的要求以及一些编码方面的原因,需要使用一些中间内存,而且计算量相对来说大了很多,因此,速度也慢了不少,上述C++的代码处理1080P的图像,需要大概7ms,经过SSE优化后的代码可以达到4ms左右的速度,这个速度在某些实时性要求比较高的场景下还是具有实际价值的。
为了进一步提高效果,在HA算法的基础上,后续还是有不少人提出了更多的改进算法,在 IPOL上,可以找到一篇
A Mathematical Analysis and Implementation of Residual Interpolation Demosaicking Algorithms
的综述性文章,文章里列举了数种类型的处理方式,那个网站是个也提供了在线的DEMO和代码,可以看到各自的处理后的结果,如下图所示:

不过这些都是比较传统的算法方面的东西了,而且我看了代码和有关效果,感觉这些算法更偏重于理论,实际操作起来,可能效率完全不够,同时IPOL上还提供了一篇基于CNN深度学习方面的算法,效果我看了下,确实还是很不错的,不过就是感觉速度比较堪忧,有兴趣可以在 A Study of Two CNN Demosaicking Algorithms 这里浏览。
那么我后面关注到的是IPOL的另外一篇文章: Zhang-Wu Directional LMMSE Image Demosaicking ,通过测试发现这个文章的效果还是非常不错和稳定的,而且分析其代码,感觉可以做很大的优化工作。
这个文章对R和B通道的处理方式是和HA算法一样的,都是先要获取G通道的全部数据,然后采用色差恒定原理计算R和B,在计算G通道时,从水平和垂直方向计算 (G-R) 和 (G-B) 的颜色差异开始。然后,这些计算被视为对实际色差的噪声估计,并使用线性最小均方误差框架将它们优化组合。
所谓的优化组合可以这样理解,传统的HA算法,在计算G通道时,就是根据水平和垂直方向的梯度,决定最后是使用水平还是垂直方向的计算值,而ZhangWu算法则不完全使用水平或垂直的信息,而且根据某些过程计算出水平和垂直方向各自的权重然后融合。
这里简单的描述了一下色差噪声估计的公式:
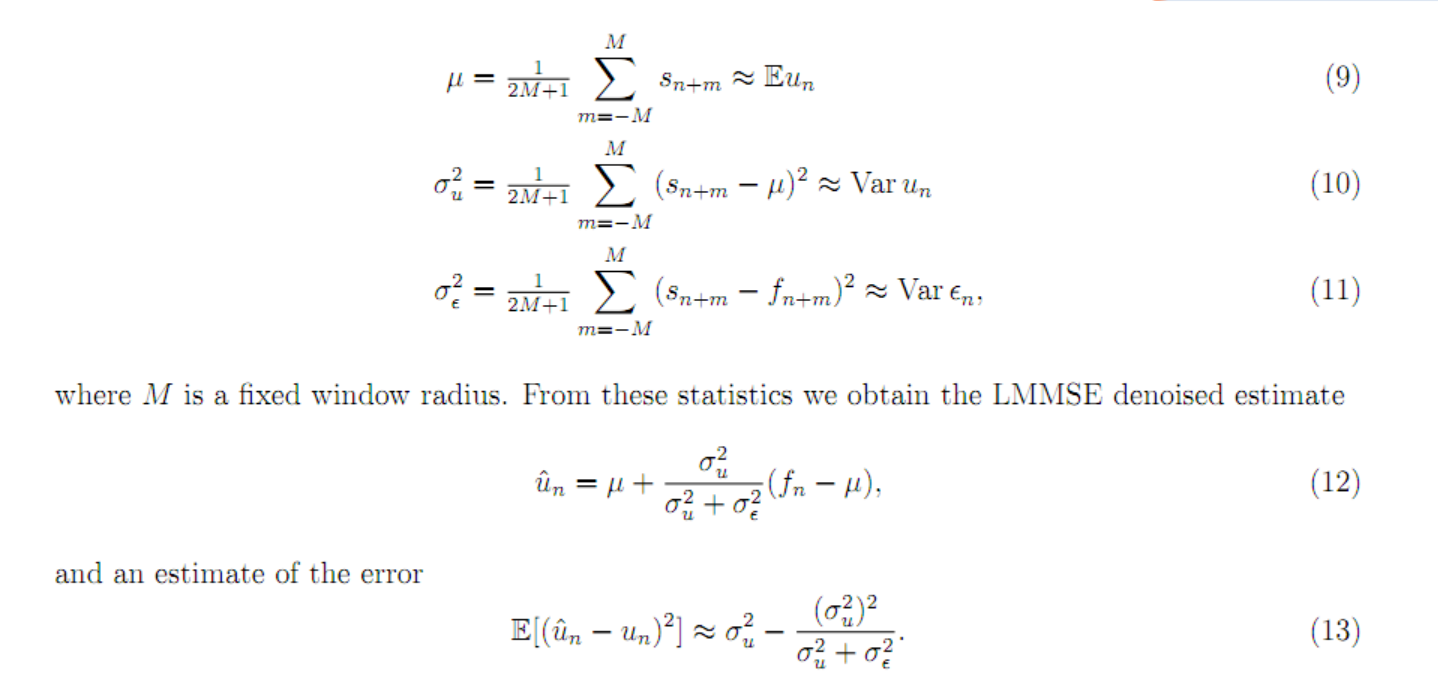
这几个公式可以看成是一个简单的去燥过程,其中f表示原始的噪音信息,s呢就是一个对f的简单的低通滤波,比如高斯滤波,然后呢公式9计算s的一定领域大小的平均值, 公式10计算s在这个领域内的方差, 公式11则计算f和s差异平方的均值。
利用以上信息则可以估算出去除噪音后的估算值 u(公式12)以及对一个的估算误差(公式13)。
分别对水平和垂直反向上的颜色差异进行这样的滤波,然后利用上面的结果按照下述公式进行融合:
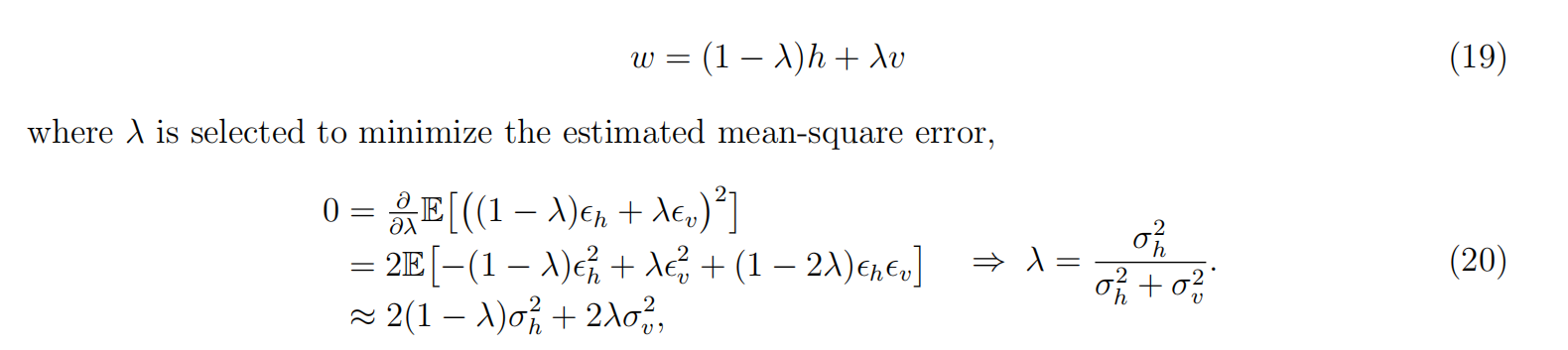
上面的公式是一个一维的去燥过程,我有空将其改为2维的图形去燥看看效果如何。
这些公式在论文的配套代码里都有有关的实现,有兴趣的朋友可以有去看看代码,我将其过程进行过程化,这个函数大概有如下代码构成:
具体的实现就不做过多的探讨,原始作者的C代码效率非常的低下,简单的测试了下1080P的图大概需要1分钟左右,这完全没有实际的意义的,所以需要进行深度的优化,比如水平方向的滤波,原作者采用1*9的滤波器,我稍作改进并用SSE指令优化如下:
这极大的提高了运行速度。
在LMMSE的计算过程中,作者的M大小取的是4,即涉及到的领域大小也是9个像素,作者在代码里使用硬循环实现,实际上这个也就是普通一进一出的统计,完全可以做点优化的,特别是垂直方向的循环,每次都要跳一行像素,cachemiss很大,所以通过适当的改动结构,能极大的提高速度。经过优化,我们测试这个算法处理处理一副1080P的图像,SSE版本大概耗时12ms,我自己优化后的C++代码耗时约27ms(使用了编译器自己的向量化方式编译,而且非原始作者的C++代码),这个速度应该说在实时系统中还是可以接受的,而且这个过程还是可以进行多线程并行化的,如果开两个线程,SSE版本有望做到8ms一帧。
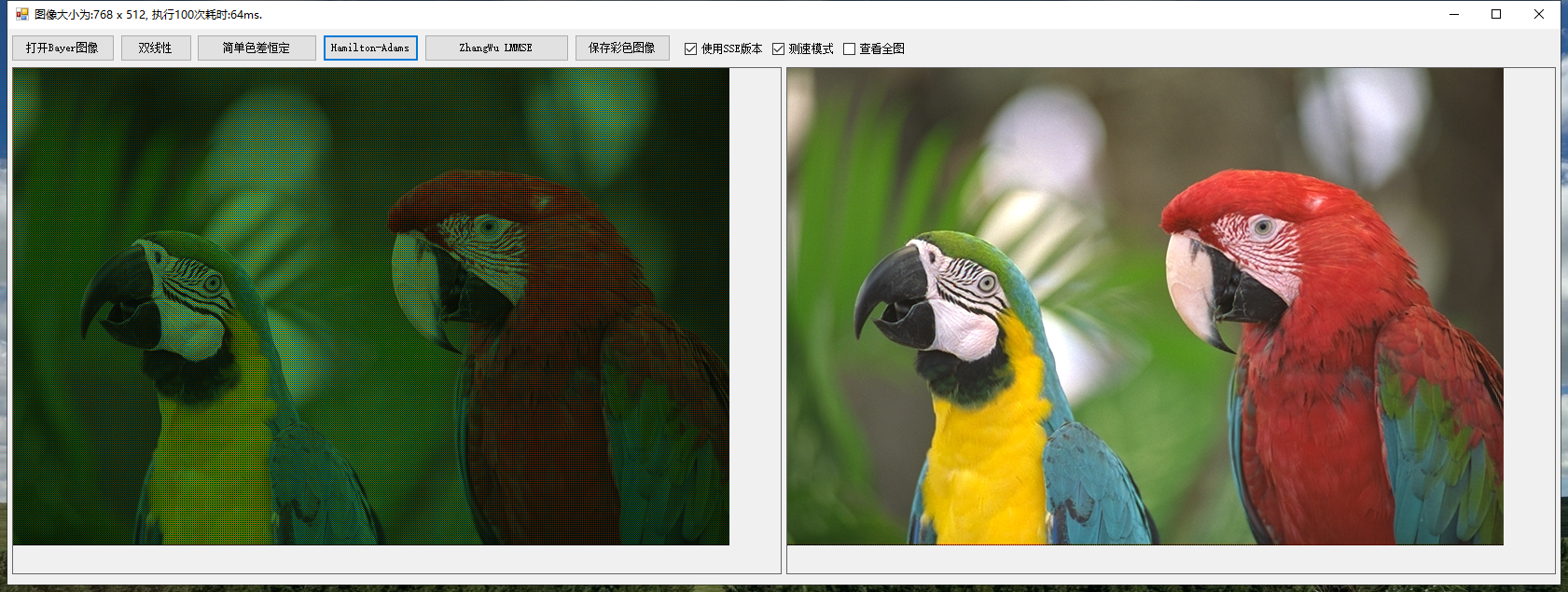
同HA算法相比,这个算法得到的结果更加完美,而且有瑕疵的地方更少,如下所示:


Zhang Wu算法结果 原始图像
我们再分享一组测试及图像:


Mosaic Bilinear


HA Zhang Wu
整体来看,效果最好是的Zhang Wu算法, 其次是HA, 最一般的就是Bilinear了,但是,也不要一板子拍死Bilinear, 在很多不是很复杂的场景的情况下,使用他得到的效果依旧是可以满足需求的,关键是他真的快啊。
当然,如果对算法执行效率和效果都要做一个均衡的话,应该说HA算法就比较适中了。
为了比较方便,我编写了一个简易的DEMO,供大家做算法验证。
https://files.cnblogs.com/files/Imageshop/DeMosaic.rar?t=1725238639&download=true
如果想时刻关注本人的最新文章,也可关注公众号:

参考资料:
// https://blog.csdn.net/OdellSwan/article/details/136887148 ISP算法 | Demosaic(一)
// https://blog.csdn.net/OdellSwan/article/details/137246117 ISP算法 | Demosaic(二)
// https://cloud.tencent.com/developer/article/1934157 ISP图像处理之Demosaic算法及相关
// https://zhuanlan.zhihu.com/p/594341024 Demosaic(二)Hamilton & Adams插值算法
// https://zhuanlan.zhihu.com/p/144651850 Understanding ISP Pipeline - Demosaicking
//
https://blog.csdn.net/feiyanjia/article/details/124366793
热门资讯